Climalteranti.it

Mentre si discute del riscaldamento globale e dei conseguenti cambiamenti climatici, può essere utile fermarsi per capire (o ripassare) l’origine del problema, ossia la presenza di un effetto serra che è un tassello fondamentale del bilancio energetico e del sistema climatico terrestre, il cui  “motore” è il riscaldamento differenziale del pianeta causato dalla radiazione del Sole.

L’energia che guida il sistema climatico proviene dal Sole: sono del tutto trascurabili (al più allo 0,03%) gli apporti dovuti ad altre sorgenti esterne (stelle o altri sistemi extrasolari) o interne (attività geotermica o combustioni antropiche). Quando l’energia del Sole raggiunge la Terra, è parzialmente assorbita da diverse componenti del sistema climatico. L’energia assorbita viene riconvertita in calore, che riscalda la Terra e la rende abitabile. L’assorbimento di radiazione solare non è uniforme nello spazio e nel tempo, e già soltanto questo fatto origina il complicato pattern termico e le variazioni stagionali del nostro clima.

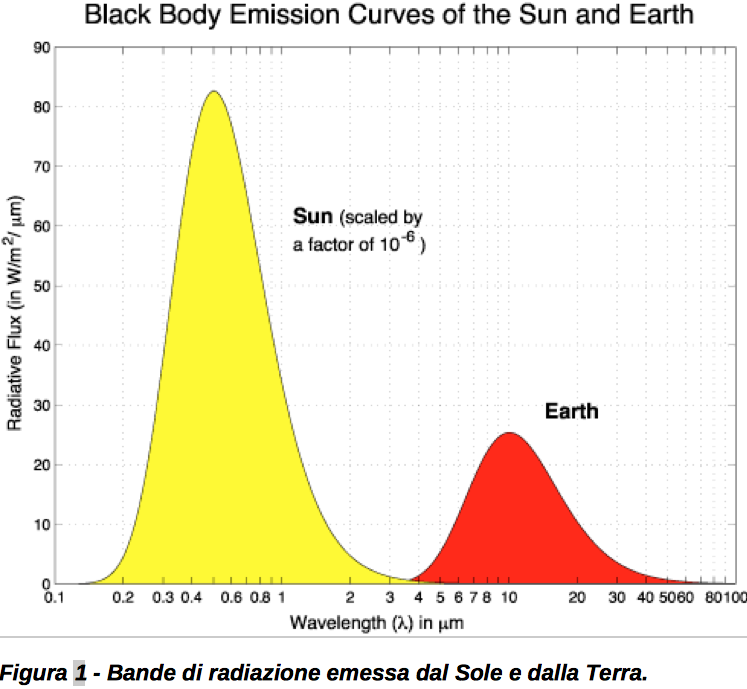
L’energia termica del Sole viaggia attraverso lo spazio sotto forma di onde elettromagnetiche che consentono il continuo trasferimento di calore attraverso un processo noto come radiazione. La radiazione solare copre un ampio intervallo di lunghezze d’onda, ma non è irradiata con la stessa intensità in tutte le bande: come si vede in Figura 1, la parte più importante dello spettro è centrata sulla banda di lunghezza d’onda 0.2-2 micrometri (un micron è un milionesimo di metro), e comprende radiazione ultravioletta (UV, nella banda 0,001-0,4 micron), radiazione visibile (luce, 0,4-0,7 micron) e radiazione infrarossa (IR, 0,7-100 micron). Il picco della radiazione solare è raggiunto alla lunghezza d’onda di circa 0.5 micron, corrispondente al colore giallo-verde. Si noti che noi “vediamo” il sole più giallo che verde poiché l’occhio umano “filtra” la radiazione verde leggermente di più rispetto a quella gialla; abbiamo detto “vediamo” tra virgolette poiché – si sa – nessun uomo dovrebbe mai guardare il sole a occhio nudo, pena la perdita permanente di una porzione non indifferente di coni e bastoncelli della retina, fino ad arrivare alla completa cecità per osservazioni di alcune decine di secondi.

Il Sole si trova al centro del Sistema Solare, a una distanza di circa 150 milioni di chilometri dalla Terra. Con una temperatura superficiale di 5780 K (i K sono i gradi kelvin, usati dai fisici, pari ai gradi centigradi °C più 273,15 °C: ovvero, 1 °C = 274.15 K). Il flusso di energia che esce dalla superficie del Sole, ovvero l’energia per unità di area e di tempo (è questa la definizione fisica di flusso) è, in media, di circa 63 milioni di Watt per metro quadro (tecnicamente 6,3 10⁷ W/m²), pari ad una potenza di 3,846 10²⁶ watt. Il processo fisico per il quale un corpo dotato di temperatura diversa da zero gradi kelvin irradia energia è noto come irraggiamento, e il rateo di emissione è regolato dalla legge di Planck.

Viaggiando nello spazio, il flusso si riduce in modo inversamente proporzionale al quadrato della distanza: questo perché la radiazione si distribuisce sulla superficie sferica di raggio r, e l’area di questa superficie aumenta come r².  Pertanto, quando la radiazione raggiunge il limite esterno dell’atmosfera terrestre (tale punto è chiamato, in inglese, TOA, ovvero Top Of Atmosphere), diverse centinaia di chilometri sopra la superficie terrestre, il flusso radiativo è di circa 1367 W/m², e questo numero è quello che è generalmente conosciuto come “costante solare”.

Se si vuole fare il conto, si può considerare che la distanza media Terra-sole è di 150 milioni di km, e quindi può dividere la potenza emessa dal sole per la superficie di una sfera di raggio pari alla distanza media Terra-Sole.

Nella realtà, ci sono due fattori che rendono variabile il flusso di radiazione che incide al TOA (e pertanto la costante solare, che quindi tanto costante non è): l’eccentricità dell’orbita di rivoluzione terrestre attorno al Sole (che modifica la distanza Terra-Sole), e la variabilità della potenza solare (che modifica la potenza emessa).

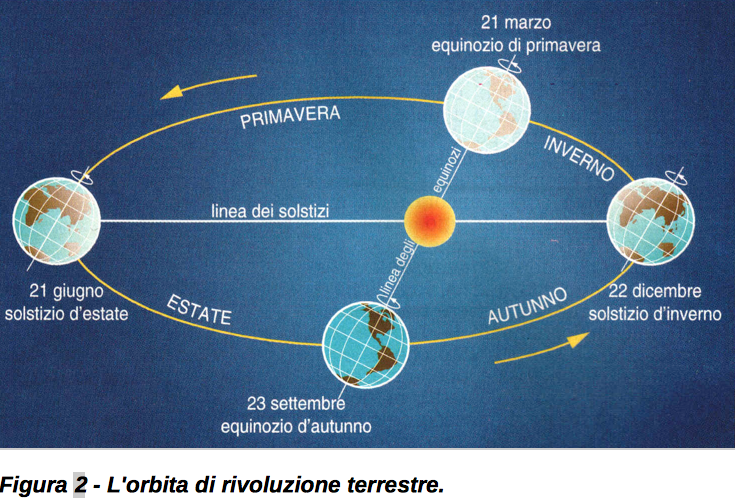
La Terra compie un movimento di rivoluzione intorno al Sole (Figura 2) mantenendosi sullo stesso piano e senza che l’asse di rotazione terrestre cambi la sua inclinazione. Il periodo del moto di rivoluzione terrestre ha la durata di 365 giorni, 5 ore, 48 minuti, 46 secondi. L’orbita è ellittica, ma l’eccentricità di questa ellissi è molto piccola. Di conseguenza, variando la distanza Terra-Sole nel corso dell’anno, varia anche la radiazione incidente al TOA, di circa il 3,5% nel corso dell’anno. La Terra è più vicina al sole in un periodo dell’anno (quando si trova in perielio: attualmente questo avviene circa a metà dell’inverno) rispetto al momento “opposto” (afelio, ad agosto).

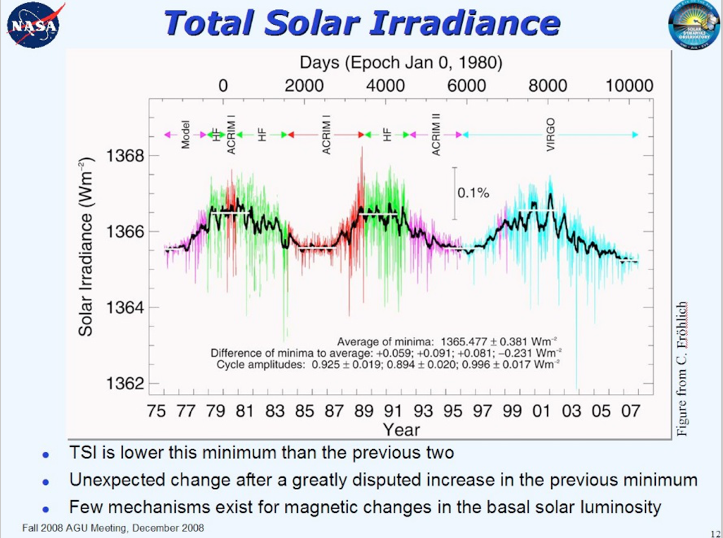
Figura 3 – misure di radiazione solare da parte di vari satelliti o modelli. Fonte: NASA.

Per quanto riguarda la potenza solare, anch’essa varia nel corso del tempo. Il più noto ciclo è quello undecennale legato alle macchie solari, il cui periodo non è in realtà esatto ma può variare tra dieci e dodici anni; ma ci sono altre ciclicità meno evidenti (80, 200, 400 e 600 anni). Come si vede dalla Figura 3, la variazione percentuale della radiazione solare media annua a seguito del ciclo undecennale è inferiore al 5‰.

Nel calcolo seguente, supponiamo che la radiazione solare al TOA sia costante e pari a 1367 W m^-2. Se la Terra fosse un disco con la superficie perpendicolare ai raggi del Sole, su ogni punto di essa arriverebbe la stessa quantità di radiazione, pari alla “costante solare”. Poiché il raggio medio terrestre è di 6371 km, complessivamente il disco riceverebbe quindi una potenza pari a 1367 x (6371000)² W.

Siccome la Terra non è un disco con la superficie perpendicolare ai raggi del Sole, ma una sfera sulla cui superficie i raggi solari giungono con varie inclinazioni, questo comporta che ogni punto della superficie terrestre, in ogni giorno dell’anno, riceva una diversa radiazione. Limitandoci per ora a considerare il TOA, in media la quantità complessiva di energia ricevuta dalla Terra è pari a quella ricevuta dal disco (in quanto, visti dal Sole, un disco perpendicolare ai raggi solari o una sfera sono indistinguibili), ma cambia ovviamente la distribuzione di tale radiazione.

La quantità di radiazione solare, S_h, in arrivo al TOA a una determinata latitudine ed a un dato istante è proporzionale al prodotto della costante solare S_r per il coseno dell’angolo zenitale θ_s, ovvero l’angolo tra la direzione dei raggi solari e la verticale.

L’integrale giornaliero di tale prodotti permette di calcolare la radiazione al TOA per ogni latitudine terrestre e in ogni giorno dell’anno (Figura 4). Poiché l’asse terrestre è inclinato con un angolo di circa 23,5° rispetto al piano dell’orbita di rivoluzione, una volta all’anno, nei due solstizi (21 giugno e 21 dicembre), i due tropici (collocati proprio alle latitudini di 23,5° N e S) ricevono perpendicolarmente la radiazione solare a mezzogiorno, mentre le aree comprese tra i due circoli polari ed i poli sono alternativamente al buio per tutta la giornata, e non ricevono quindi radiazione solare.

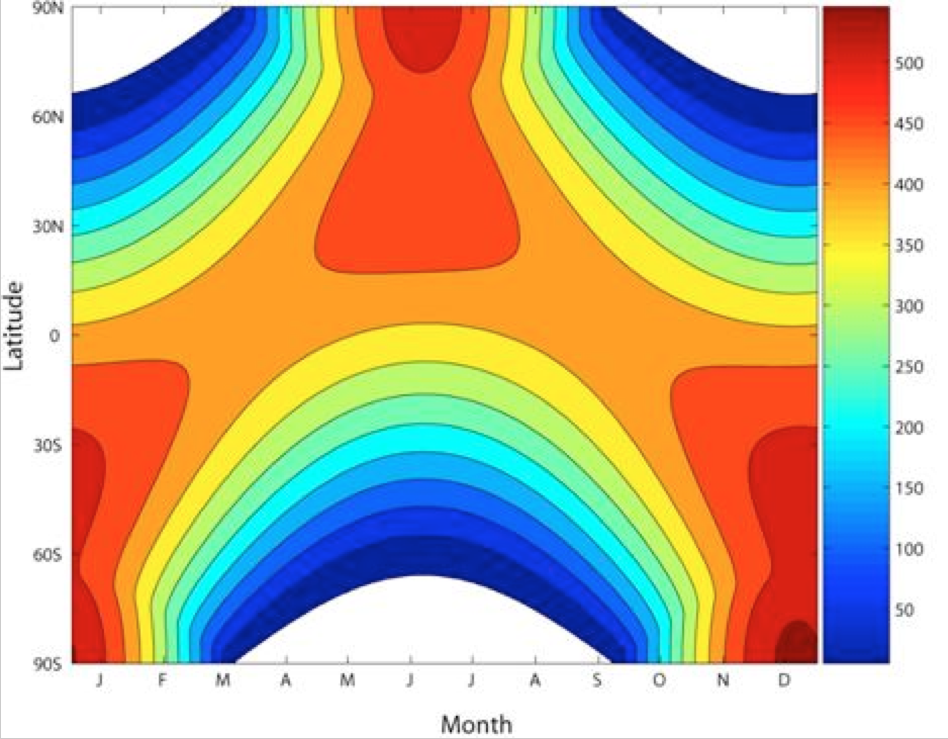
Figura 4 – Valore medio giornaliero della radiazione al limite esterno dell’atmosfera per ogni latitudine e mese dell’anno.

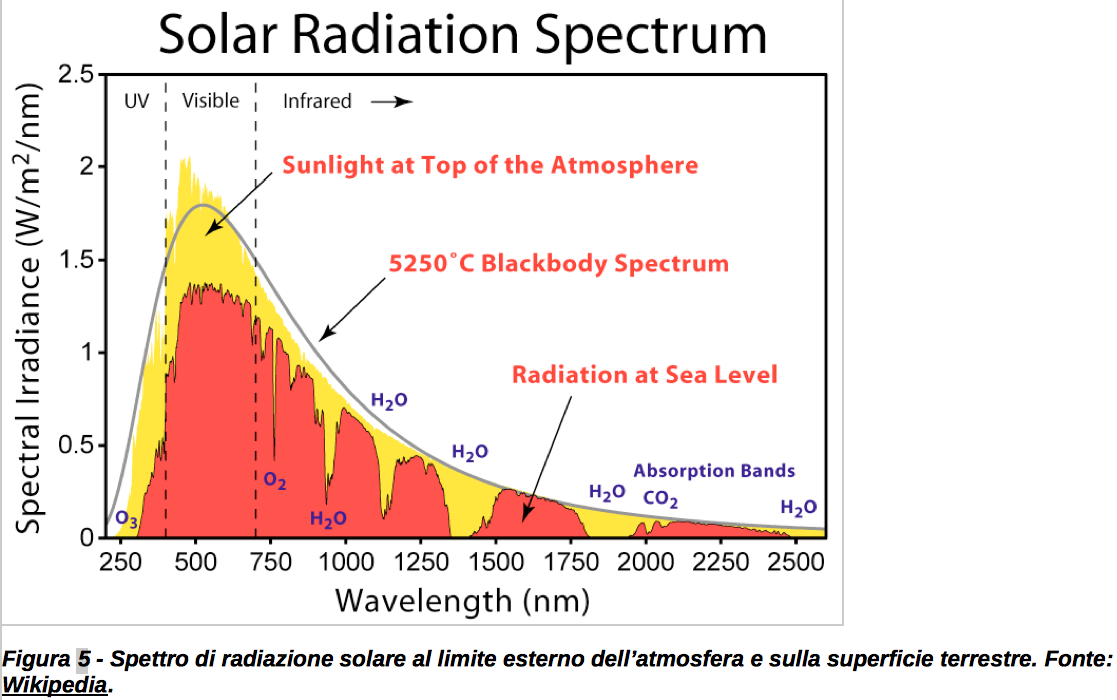
Fino a qui, abbiamo considerato soltanto la radiazione solare in arrivo al TOA. L’energia in arrivo viene in parte riflessa (dalla superficie terrestre o dall’atmosfera) e in parte assorbita. L’assorbimento è diverso a seconda delle bande di lunghezza d’onda: la Figura 5 riporta la differenza tra la radiazione media proveniente dal Sole che indice al TOA (in giallo) e quella che arriva a terra, evidenziando le varie finestre spettrali e le principali bande di assorbimento, principalmente ad opera del vapore acqueo e dell’ozono.

Il rapporto tra energia riflessa ed energia incidente rappresenta la riflettività, parametro adimensionale che i meteo-climatologi preferiscono chiamare albedo, dal latino albidus o albedine (bianchezza), e si esprime in frazioni di unità o in percentuale. L’albedo media della Terra è di circa 0,3 e questo significa che il 30% dell’energia solare incidente viene riflessa nello spazio, mentre il 70% è assorbita dalla Terra. L’albedo del pianeta non è costante né nel tempo né nello spazio, ma varia di giorno in giorno e da luogo in luogo; il valore 0,3 rappresenta pertanto il dato medio globale del pianeta.  Tale 30% di energia riflessa, come mostrato in Figura 6, è costituito da riflessione dall’atmosfera (6%), riflessione dalle nubi (20%) e riflessione dal suolo, terreno, acqua e ghiaccio (4%).

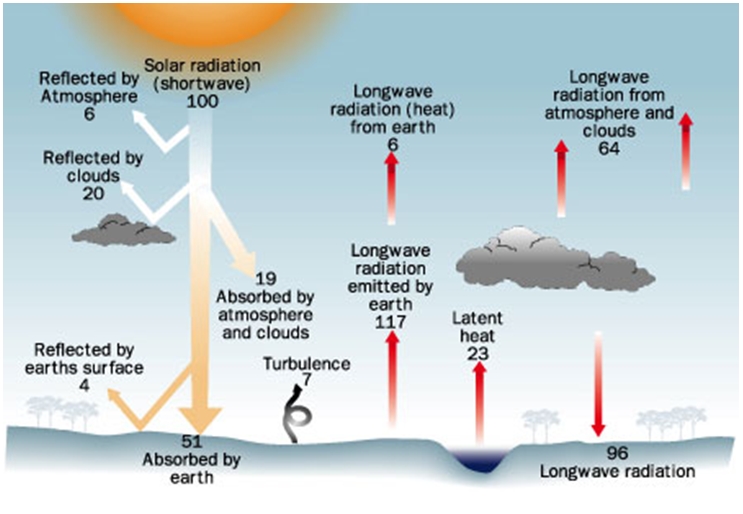
Figura 6 – Bilancio energetico della Terra: in giallo è mostrata la componente solare, ad onda corta, mentre in rosso quella infrarossa, ad onda lunga. Fonte: Crowder

Si noti come in Figura 6 la radiazione entrante sia indicata come 340 W/m² invece che 1367 W/m²: il motivo è che il numero indicato ingloba già il rapporto ¼ tra l’area di un cerchio e l’area di una sfera con lo stesso raggio del cerchio (340 ≈1367/4).

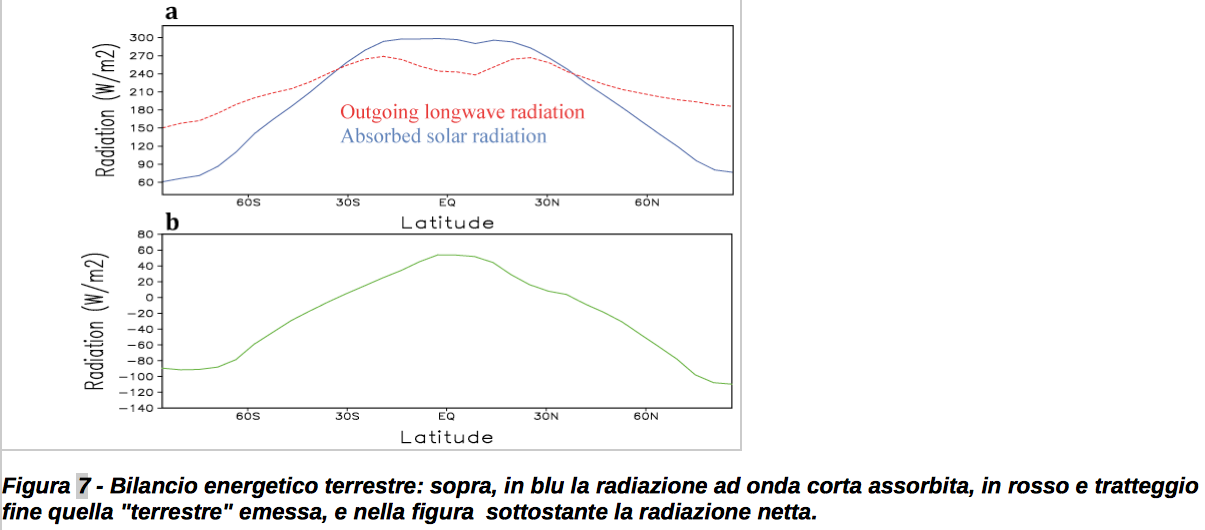
Il restante 70% dell’energia incidente è assorbito dalla superficie terrestre (51%) e dall’atmosfera (19%). Pertanto, a causa dell’albedo, dei circa 1367 W/m² medi che incidono ortogonalmente sul TOA, a terra ne arrivano soltanto 1004, distribuiti non uniformemente in quanto la copertura nuvolosa non è uniforme. Considerando poi l’inclinazione dei raggi alle diverse latitudini, e calcolando la media annua per ogni latitudine, si ottiene un andamento quasi sinusoidale come quello rappresentato dalla linea azzurra nel grafico in alto della Figura 5.

Veniamo ora al sistema Terra-Atmosfera-Oceani (nel seguito, per brevità diremo semplicemente Terra). Anche la Terra è un corpo che irradia seguendo le stesse leggi della radiazione, ovvero la legge di Planck. Poiché la temperatura della Terra è molto inferiore a quella del Sole (la temperatura media della Terra è di 15°C, ovvero circa 278 K), la radiazione emessa dalla Terra segue una curva di Planck che ha il suo picco a lunghezze d’onda molto maggiori rispetto a quella del Sole (Figura 1): la banda è infatti posizionata nell’infrarosso, e viene chiamata “ad onda lunga” perché la sua lunghezza d’onda è maggiore. Inoltre, siccome la temperatura della superficie terrestre varia considerevolmente, e siccome l’integrale della radiazione emessa a tutte le lunghezze d’onda segue la legge di Stefan-Boltzmann , che prevede una proporzionalità dalla temperatura alla quarta potenza, se ne ricava che posti situati a diverse latitudini irraggiano diversamente. A titolo di esempio, una località artica o antartica con temperatura superficiale di -50 °C irradia, nell’ipotesi di corpo nero, come σ T⁴ (con σ=5,67 10-8 Wm^-2K^-4), ovvero circa 141 W/m²; una località nel deserto sahariano avente una temperatura superficiale di 40 °C irradia circa 545 W/m².

L’atmosfera intercetta una gran parte di questa radiazione emessa dalla superficie del pianeta, e questo è proprio il meccanismo fisico conosciuto col nome “effetto serra”, perché ricorda quanto succede con i vetri di una serra. Studiato già nel XIX secolo (come raccontato qui), è un meccanismo complesso, che avviene in particolare nei bassi strati, e in particolare quando l’atmosfera è ricca di vapore acqueo (oltre che dei gas serra), e che la riemette in parte verso il basso ed in parte verso l’alto.

Un’altra complicazione  è che né la superficie terrestre, né l’atmosfera sono rigorosamente dei corpi neri, ma al più dei corpi grigi, il flusso netto reale di energia ad onda lunga varia lungo la latitudine come mostrato dalla linea rossa tratteggiata nel primo grafico della Figura 5. In particolare, è evidente come il gradiente della radiazione a onda lunga sul globo terrestre sia minore rispetto a quello della radiazione ad onda corta.

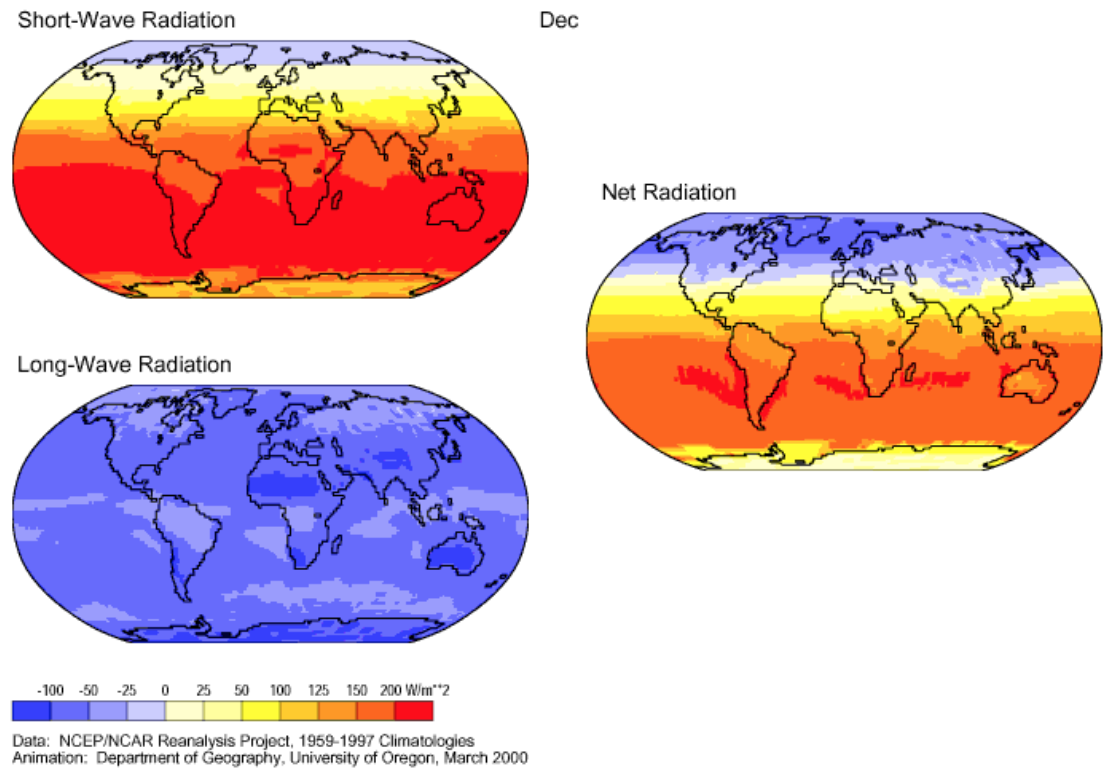
Ne consegue pertanto che, facendo ora la differenza tra l’energia netta entrante, a onda corta, e quella uscente, cioè a onda lunga, si ricava la cosiddetta radiazione netta, ovvero il flusso di energia che giunge sulla superficie terrestre: esso è mostrato nel grafico inferiore della Figura 5. Come si vede, soltanto una porzione della superficie terrestre possiede un bilancio “positivo”, ovvero riceve più radiazione di quanta ne perda. In Figura 8 si può osservare come variano, sulla superficie terrestre e nei vari periodi dell’anno, le varie componenti ed il bilancio.

Questo “sbilancio” di radiazione netta, dovuto principalmente al riscaldamento differenziale del sistema Terra-Atmosfera (a causa della diversa inclinazione con cui i raggi solari giungono sulla superficie terrestre), varia più o meno sinusoidalmente con la latitudine (in realtà occorre considerare la diversa nuvolosità delle aree del globo, ma il discorso generale non cambia). Il risultato che ne deriva è che ai poli vi è un deficit radiativo, mentre all’equatore vi è un surplus. Questo difforme input energetico deve potersi ridistribuire su tutto il pianeta, dalle basse alle alte latitudini. Se così non fosse, il sistema Terra-Atmosfera si allontanerebbe dall’equilibrio termodinamico in maniera irreversibile (e catastrofica), e come risultato la vita sulla Terra sarebbe totalmente compromessa (o forse non si sarebbe mai sviluppata): in sostanza arrostiremmo nelle aree equatoriali e tropicali e geleremmo a latitudini più elevate. Per nostra fortuna le grandi circolazioni dell’atmosfera e degli oceani permettono di ridistribuire l’energia, e tale processi sono modulati e guidati da una miriade di processi, che attivano tantissimi fenomeni operanti a tutte le scale spazio-temporali, da quelle più brevi dei giorni, settimane e pochi mesi, tipiche dei fenomeni meteorologici, a quelle più lunghe, quelle degli anni anni e dei decenni,  studiate invece dalla climatologia.

.

Testo di Claudio Cassardo e Carlo Cacciamani

Tags: Plank, Stefan-Boltzmann

. Climalterantə on Mag 7th 2014 Categorie: Bilancio radiativo, Effetto Serra, Energia, Fenomenologia, Sole, TemperatureStampa questo articolo